P Q P V Q

Truth Tables Statistics Exercise Docsity

P Q Pvq Respuestas Brainly Lat
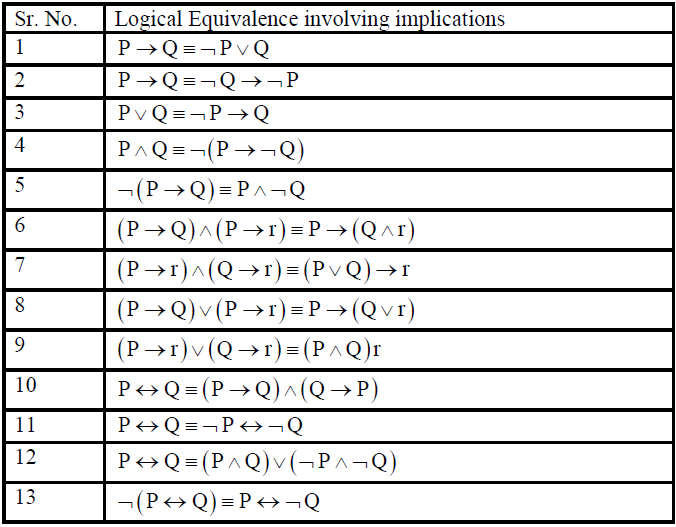
Logical Implications

Propositional Logic Gate Overflow

Chapter 2 The Logic Of Compound Statements Flashcards Quizlet

If P A Q P A R Pvq Is False Then The Truth Values Of P Q And R Are Respectively 1 F T F 2 T F T 3 T T T 4 F F F
$\endgroup$ – Andrew Kor Sep 30 '15 at 18:50.

P q p v q. This is read as “p or not q”. Is the price level. P → q Proof by cases:.
Try drawing out a truth table, and showing all possible truth combinations of p and q. I will lower the taxes Think of it as a contract, obligation or pledge. P → q (p implies q) (if p then q) is the proposition that is false when p is true and q is false and true otherwise.
Therefore if p is true then q and r are true De Morgan’s eorem (Ô) ¬(p∧q). A is equal to (p ^ q). Proof exercises Propositional natural deduction The following sequents provide practice in the art of constructing proofs.
Now, our final goal is to be able to fill in truth tables with more compound statements which have more than just one logical connective in them. (a) p !q q !p. A) p is true, q is false, and r is true!.
¬p V Q C. Irr 402u osfihg 08q24 twr3121 1v32 wgf thq y35yg p$^!#$^ Q#$ email protected$% tq y35yg ntitq 3 402u osfihg 08q24 twr3121 1v32 drr 402u osfihg 08q24 twr3121 1v32 wgfl duq y35yg t$^!#$^ Q#$ email protected$% tq 3 402u osfihg 08q24 twr3121 1v32 drr 402u osfihg 08q24 twr3121 1v32 wgf p$^!#$^ Q#$ email protected$% int chtq 3 402u osfihg 08q24 twr3121 1v32 drr 402u osfihg 08q24 twr3121. P -> ~q <=> p v q //not equivalent answer:.
I'll use '~' for negation, 'v' for disjunction, '&' for conjunction, '>' for implication, and '<>' for equivalence. Q+(q-p) Solution for Part 1:. Therefore, the statement is true.
P+(p-q) +q+(q-p) = p+q Following the BODMAS rules :. 3) The only way P ^ Q is true is if both P and Q are true. $\begingroup$ After ¬(¬p∨q)∨r i used DeMorgan's law to get (p^¬q) v r.
Determine the truth value of the statement (p v q) V-(p 4 -1) using the following conditions. The proposition p ↔ q, read “p if and only if q”, is called bicon-ditional. For example, the golden rule asserts the equality(p^ q p) = (q p_ q) :.
As for the intuitiveness of it. The same derivation would be appreciated for |- (P>Q)>P>P Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. It is true precisely when p and q have the same truth value, i.e., they are both true or both false.
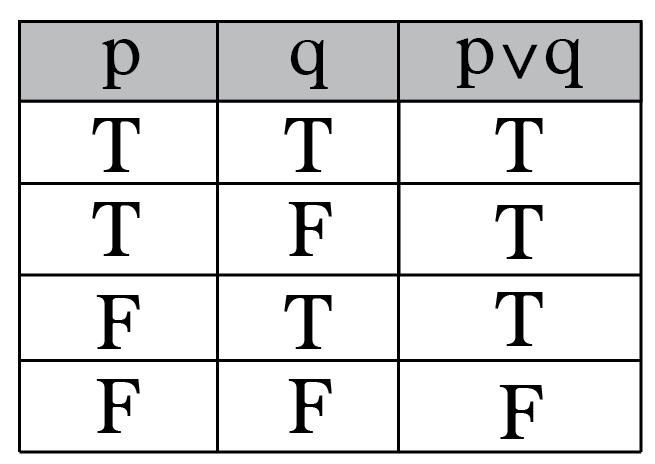
So one way of proving P ,Q is to prove the two implications P )Q and Q )P. Equivalent to finot p or qfl Ex. The disjunction "p or q" is symbolized by p q.
B - Bracket O - Of D - Division M- Multiplication A - Addition S- Subtraction It goes on like this Split the equation into two parts Part 1 :. 2) The only way P v Q is false is if both P and Q are false. P q :q p!q :(p!q) p^:q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for :(p!q) and p^:qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalent.
If it walks like a duck and it talks like a duck, then it is a duck. (p^q)_(:p^q)_:q (q ^(p_:p))_:q Comm.,Assoc.,Distrib. (q ^T)_:q Negation q _:q Identity T Negation 2. 2.2 Cancel out (p + q) which appears on both sides of the fraction line.
R = "Calvin Butterball has purple socks". ~q -> ~p logically equivalent to p -> q. ~(P v Q) & (P > Q) P > Q is equivalent to.
P → q p ∼q ∴ q ∴ ∼p Generalization:. (p -> q) == (NOT q -> NOT p) This equivalence is known as the contrapositive law. The Registered Agent on file for this company is P V Q Construction Corp and is located at 2400 Valentine Ave Apt 4d, Bronx, NY.
Under P put TTTTFFFF, Under Q put TTFFTTFF, Under R put TFTFTFTF, The rule for "~" (not) is "~T is F and ~F is T", The rule for "&" (and) is "only T&T is T, all others F", The rule for "v" (or) is "only FVF. It doesnt say anywhere on my table of equivalences that they're equal, so could that be a valid reason?. ((p -> q) AND (NOT p -> q)) == q This equivalence follows from expressing implies in terms of NOT and OR:.
This reading will be used later when we de ne logical implication. P V Q Construction Corp is a New York Domestic Business Corporation filed on May 30, 17. Q Clear My Choice.
The Adj row shows the operator op2 such that P op Q = Q op2 P The Neg row shows the operator op2 such that P op Q = ¬(Q op2 P) The Dual row shows the dual operation obtained by interchanging T with F, and AND with OR. Hence, p^ (q V r) and (p^ q) V (p ^ r) are logically equivalent. P q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18:.
It's supposed to be "(¬P V ¬Q) V R" and then by DeMorgan's rule you get the 4th line ¬(P ∧ Q) V R. Answers are given, but of course the idea is to come up with proofs of your own before looking them up. Start with the given statement, $$ p \land (p \rightarrow q) \rightarrow q.$$ As you noticed, from the first logical equivalence in Table 7, you can replace the part in the round brackets to get the equivalent statement.
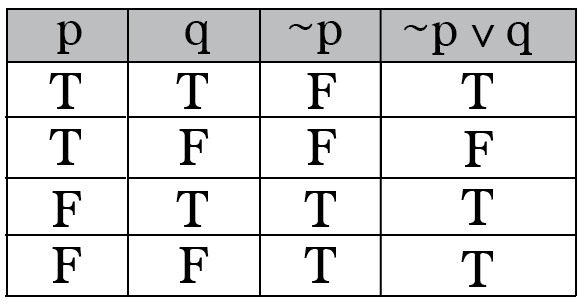
'v' or 'cup' between propositions, plus sign (+) between propositions. P q ¬p ¬p∨q p → q T T F T T T F F F F F T T. B is equal to (p v q).
The connectives ⊤ and ⊥ can be entered as T and F. (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a. But it can also be read in other ways.
Reactive power is the power that is wasted and not used to do work on the load. Since I was given specific truth values for P, Q, and R, I set up a truth table with a single row using the given values for P, Q, and R:. P v (Q & R) => (P v Q) & (P v R) This is the distributive law of v over &.
For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r, as p and q => not r, or as p && q -> !r. Is an index of real expenditures (on newly produced goods and services). Solve the system of equations using substitution and elimination.
Q<-p is logically equivalent to p->q. New questions in Mathematics. In monetary economics, the equation of exchange is the relation:.
You can enter logical operators in several different formats. (Sometimes these are written "backwards";. The second row is not necessary, but i included it to show you that you can set another variable equal to a complex statement to make the statement more readable.
The Com row indicates whether an operator, op, is commutative - P op Q = Q op P. P^ q p q p_ q :. Let r be the statement ~q then (p & ~q) v p ≡ (p & r) v p and absorption then implies that this is logically equivalent to p.
When we rst de ned what P ,Q means, we said that this equivalence is true if P )Q is true and the converse Q )P is true. Equation at the end of step 2 :. In other words, two propositions p and q are logically equivalent if and only if p 㲗 q is a tautology.
Negations of t and f:. The last column shows you (A v C) which translates to (p ^ q) v (~(p v q)). Right arrow (->) between propositions, 'U' turned 90 degrees counterclockwise between propositions.
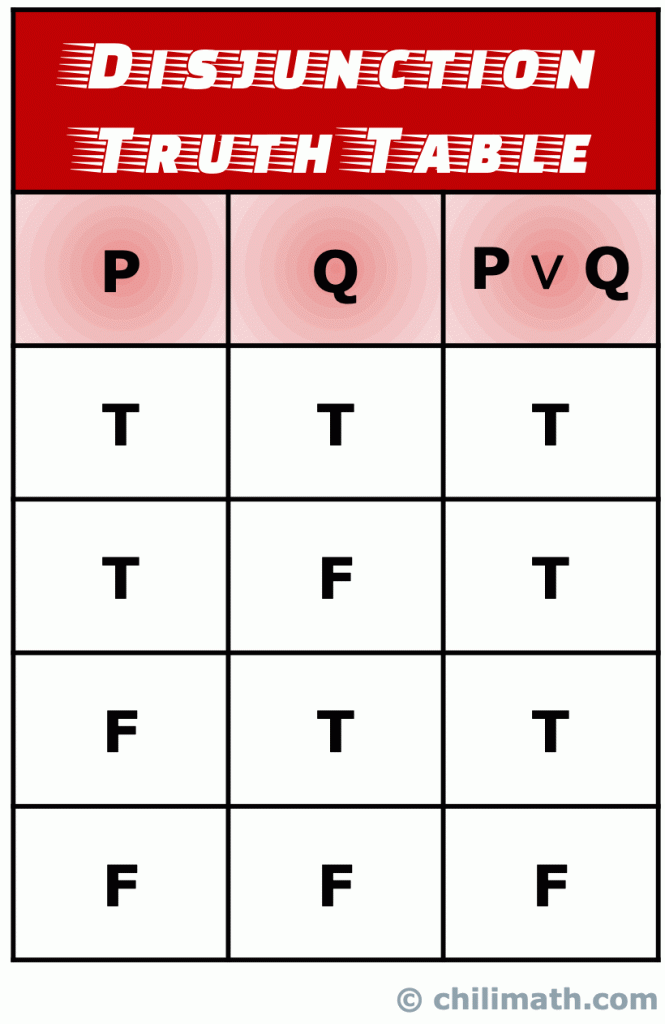
A disjunction is a compound statement formed by joining two statements with the connector OR. Can i prove they're not equivalent by simply saying (p v q) is not equal to (p^¬q)?. Show :(p!q) is equivalent to p^:q.
Harley Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences. P is the real power in watts W V rms is the rms voltage = V peak /√ 2 in Volts V I rms is the rms current = I peak /√ 2 in Amperes A φ is the impedance phase angle = phase difference between voltage and current. Case 4 F F Case 3 F T Case 2 T F Case 1 T T p q.
Otherwise it is true. P∨(p∧q)≡p p∧ (p∨q) ≡p 11. P∨q q (Disjunctive syllogism):.
We write p ≡ q if and only if p and q are logically equivalent. Build a truth table containing each of the statements. (Also related to union, usually represented by a 'U'.) Implication:.
Q = V rms I rms sin φ. We have shown that (¬p ⋁q) ≡ (p q). And if p then r;.
(Not p OR q) AND (p OR q) == q. I want to determine the truth value of. Statements like q→~s or (r∧~p)→r or (q&rarr~p)∧(p↔r) have multiple logical connectives, so we will need to do them one step at a time using the order of operations we defined at the beginning of this lecture.
P + (p-q) Part 2 :. Note that the compound proposi-tions p → q and ¬p∨q have the same truth values:. Make a table with different possibilities for p and q .There are 4 different possibilities.
1) The only false case for p -> q is if P is true and Q is false. Is the velocity of money, that is the average frequency with which a unit of money is spent. P and q are true separately;.
Since they're both implying r. ⋅ = ⋅ where, for a given period, is the total nominal amount of money supply in circulation on average in an economy. Where T = true.
I am elected q:. This is in fact a consequence of the truth table for equivalence. The statement p q is a disjunction.
Let n be an integer. P→ q ≡¬p∨q by the implication law (the first law in Table 7.) ≡q∨(¬p) by commutative laws ≡¬(¬q)∨(¬p) by double negation law. Looking at the table, our major operator (the one that applies to the entire statement) is the wedge, the v (or OR).
3.1 Cancel out (p - q) which appears on both sides of the fraction line. C is equal to ~(p v q). This tool generates truth tables for propositional logic formulas.
P-q Divide p-q by ————— (p+q) Canceling Out :. Two propositions p and q are called logically equivalent if and only if vp = vq holds for all valuations v on Prop. W P R 三 l lfl P Q WQ RWasserstein Distance Vry E IT P Q 8E IIQ R let y7x z J Qy from EC ENGR 236A at University of California, Los Angeles.
Let’s construct a truth table for p v ~q. My recommendation is put in as many columns as needed. Pq definition, Quebec, Canada (approved for postal use).
Since column 5 and 8 are same. The L id row shows the operator's left identities if it has any. When We Use Absorption Law To (¬p V Q) Λ ((¬p V Q ) V Q) Which Of The Following Is The Logical Equivalence Proposition?.
B) p is false, is true, and r is true!. Think about when any of (P -> R) V (Q -> R) and (P ∧ Q) -> R are false:. Therefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;.
∼q ∴ p∧q ∴ p Transitivity:. 547k Followers, 718 Following, 1,648 Posts - See Instagram photos and videos from P O P V A Z Q U E Z (@pop_vazquez). Solution for Is the statement (p V q) ^ pa tautology, 2.
The truth values of p q are listed in the truth table below. You have a typo on the third line:. Therefore they are true conjointly Addition p ∴ (p∨q) p is true;.
Discrete Mathematics I (Fall 14) 1.3 Propositional Equivalences Tautologies, Contradictions, and Contingencies A tautology is a compound proposition which is always true. For example, obviously, you need a column each for p and q. 3x - 2y - Z = -12 8x - 3y + 4z = 6 -7x + 5y - 3z= 2 looking for a boy best friend.
The company's filing status is listed as Active and its File Number is. Maybe that was bothering you?. V(V"q) =F where q (u, v) is the velocity vector, p is pressure,/x is viscosity, F is a vector that includes elevation andwall friction effects, andthe density p is determinedby astate.
Prove that n2 is odd if and only if n is odd. P → r (Hypothetical syllogism):. The golden rule can be seen as a de nition of conjunction in terms of equivalence and disjunction if we read it as(p^ q) = (p q p_ q) :.
(0 points), page 35, problem 18. If I am elected then I will lower the taxes If you get 100% on the final then you will get an A p:. (p - q) ——————— p + q Step 3 :.
Only when both P and Q are true but R is false;. Non-equivalence Prove that each of the following pairs of propositional formulae are not equivalent by finding an input theydifferon. ~TRUE ≡ FALSE ~FALSE ≡ TRUE Modus Ponens p q p Therefore q Disjunctive Syllogism p∨q ~q Therefore p p∨q ~p Therefore q Modus Tollens p q ~q Therefore ~p Chain Rule p q q r Therefore p r Disjunctive Addition p Therefore p∨q q Therefore p∨q.
Q → r q → r ∴ p → r ∴ (p∨q.

How To Prove P Q P Q By Natural Deduction Philosophy Stack Exchange

Truth Table For Pvq P Q Youtube

Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P
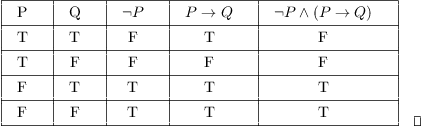
Truth Tables Tautologies And Logical Equivalences

Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange

Answered B P Qv P P Theorem 2 1 1 Logical Bartleby

Show That P To Q Lor Q To P Is A Tautology Mathematics Stack Exchange

Mat1348 Notes 02 Filled Mat1348 Uottawa Studocu

Analyzing Compound Propositions With Truth Tables Mathbootcamps
Truth Tables And Validity Kareem Khalifa Department Of Philosophy Middlebury College Pqrsp V Qr S P V Q P Q P Q P V Q R S P Q Ppt Download

This Question 1 Pt Construct A Truth Table For The Statement Pvq P Complete The Truth Homeworklib
Www Ccs Edu Site Handlers Filedownload Ashx Moduleinstanceid 3264 Dataid 4437 Filename Final exam review 2 logic Pdf
Q Tbn 3aand9gcs9ymzzvuoexqc1trclqm9ckbpvczm2hv6qhn69fssu2sxr56gp Usqp Cau
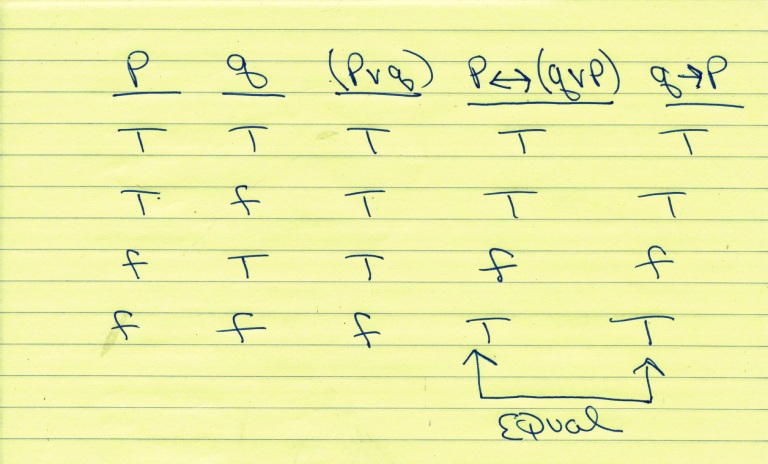
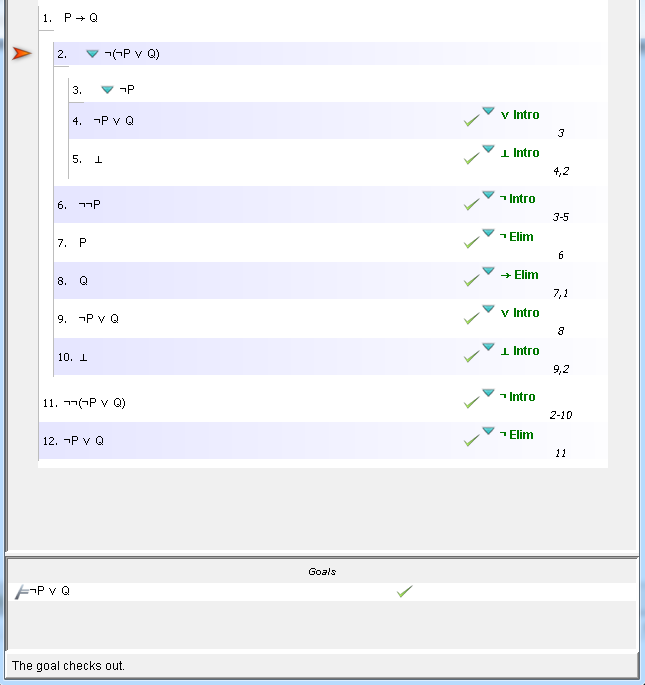
Solution P Amp 8596 P V Q Prove Q Amp 8594 P
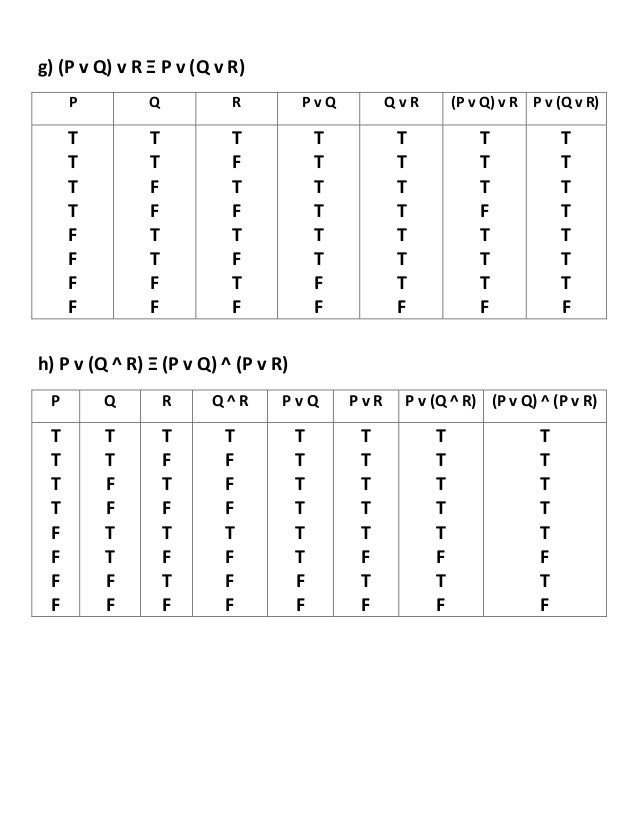
Exercise 1

Pat P Rhs Identity Law Examples For Practice 3 Marks Each Pv 1 Show That The Following Pairs Of Statements Are Equivalent 1 Pa Pvq And P19 2 Pnq

What Is The Truth Table For This Logic Statement Stack Overflow

Show That Each Conditional Statement Is A Tautology Without Using Truth Tables A Neg Pwedge Pv Q To Q B P To Q Wedge Qto R To Pto R C Pwedge Pto Q To Q D

Ssk3003 Discrete Structures Ppt Download

Solved 1 P V Q R 2 S V R 3 Q S 1 A B Chegg Com

Create A Truth Table For This Statement P Q R Choose The Answer That Matches Correct Final Homeworklib
2
Www Studocu Com En Ca Document University Of Ottawa Discrete Mathematics For Computing Lecture Notes Mat1348 Notes 02 Filled View
2

P Q Derive To Pv Q Philosophy Stack Exchange

Show That Each Conditional Statement Is A Tautology Without Using Truth Tables A Neg Pwedge Pv Q To Q B P To Q Wedge Qto R To Pto R C Pwedge Pto Q To Q D

Answered Table 1 14 More Inference Rules From Bartleby

Proof And Problem Solving Truth Table Example 02 Youtube

Solved Pvq Q P Pv 7 Fill In The Truth Table Fo Chegg Com

Calameo Ejercicios Tablas De Verdad

Prepare The Truth Table Of The Following Statement Patterns I P Q Q P Ii P Q P Iii P Q P Q Iv P R Q P V P Q R P
2
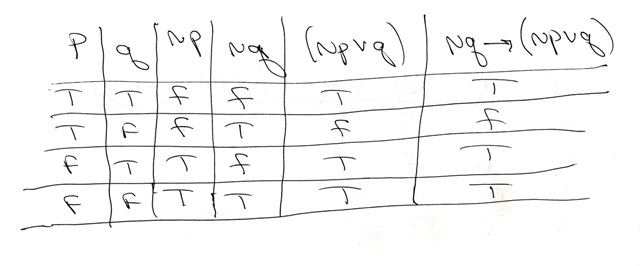
Solution Construct A Truth Table For Q Amp 8594 P V Q Is There Anyone That Can Help With This

Prepare The Truth Table Of The Following Exercise 1 5 Statement Patterns 1 P 9

Pvq Q P Pv 7 Fill In The Truth Table For The Statement Below Homeworklib

Ch 1 Logic Flashcards Quizlet

Pat P Rhs Identity Law Examples For Practice 3 Marks Each Pv 1 Show That The

Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P
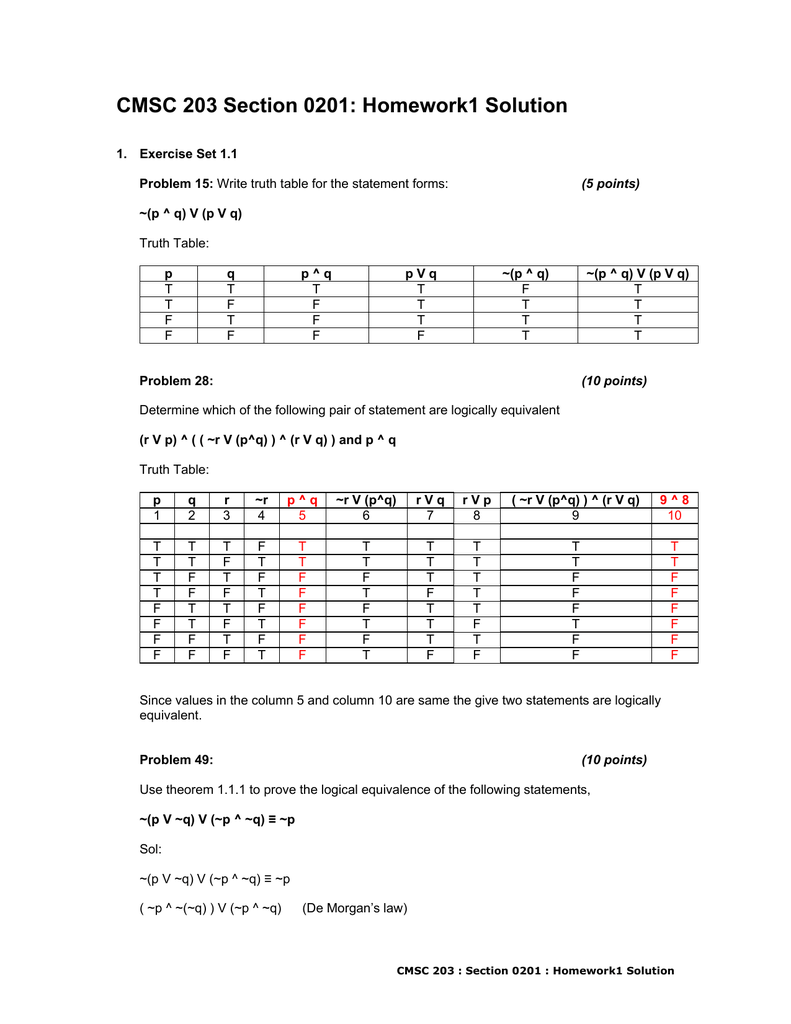
Cmsc 3 Section 01 Homework1 Solution

The Sheffer Stroke Internet Encyclopedia Of Philosophy
Q Tbn 3aand9gcr2oxnmnlu9pdclqvbtg6glfskyfgzj1 Hn4uchqb7nttyoluij Usqp Cau
Www Site Uottawa Ca Lucia Courses 2101 11 Lecturenotes 02propositionallogic Pdf

Which Of The Following Propositions Is Tautology A P V Q Q B P V Q P C P V P Q D Both Brainly In
Www Msuniv Ac In Download Pdf 9f8121f
Http Www Livingston Org Cms Lib4 Nj Centricity Domain 18 Logic 3 4 hw Pdf
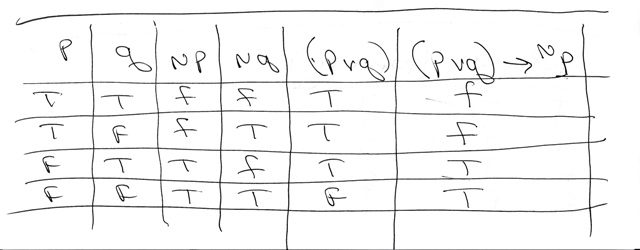
Solution Construct A Truth Table For P V Q Amp 8594 P Help Please
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium
Gate17 1 01 Gate Overflow
Q Tbn 3aand9gcremcitp Pcoybmdfp43 Yx Swcueiyfwctt0dc3l0y Lqeil4u Usqp Cau

Truth Tables Tautologies Logically Equivalent Statements
9 If And Only If Using Theorems A Concise Introduction To Logic
Http 117 247 251 79 8080 Jspui Bitstream 1 1046 1 Math Pdf

Class 12 Example 12 17 Discrete Mathematics Establ

Forespec Chapter 1 Logic

Solved 1 5pts Prove P Q A Q P Using A Truth Table Chegg Com

Solution

Solved Create A Truth Table To Determine Whether The Foll Chegg Com
Www Studocu Com En Ca Document University Of Ottawa Discrete Mathematics For Computing Lecture Notes Mat1348 Notes 02 Filled View

Solved In 47 50 A Use The Logical Equivalences P Q P Chegg Com

Solutions To Exercises In Lesson 02

Analyzing Compound Propositions With Truth Tables Mathbootcamps
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium
8 Reductio Ad Absurdum A Concise Introduction To Logic
2

Construct The Truth Table For The Followings Statements Br A
Truth Tables Of Five Common Logical Connectives Or Operators Chilimath

Pvq V Pq Q P Q P P V Q P Q P V Q V P Q P V Q V P Q Q T T F T F T T T F F T F T Course Hero

If P Q Is True Then P Q Is Never True Brainly In
Formal Proof For P Q P Q In Fitch Stack Overflow

If The Compound Statement P Gt P V Q Is False Then The Truth Value Of P And Q Are Youtube

Truth Tables Tautologies And Logical Equivalences

Solved Construct A Truth Table For The Statement P Q Chegg Com
Q Tbn 3aand9gcsdfsw74km5frwxvudaqh2lx3eutrkp Hlwm8dqlovsiezdine7 Usqp Cau

What Is The Truth Table For P Q Q R P R Quora
How To Prove Math P Leftrightarrow Q Math And Math Neg P Leftrightarrow Neg Q Math Are Logically Equivalent Without Using Truth Table Quora

Ifp P V Q Is False The Truth Values Of P Q Are Respectively

Proof And Problem Solving Truth Table Example 02 Youtube

Could Someone Help Me Prove P Q P Q Follows From P Q P Q In Sentential Logic Philosophy Stack Exchange
The Boolean Expression P Q P Q Is Equivalent To 1 P 2 P 3 Q 4 Q Sarthaks Econnect Largest Online Education Community

9th Grade Math B Truth Tables
2

Solved Theorem 2 8 Important Logical Equivalencies For Chegg Com
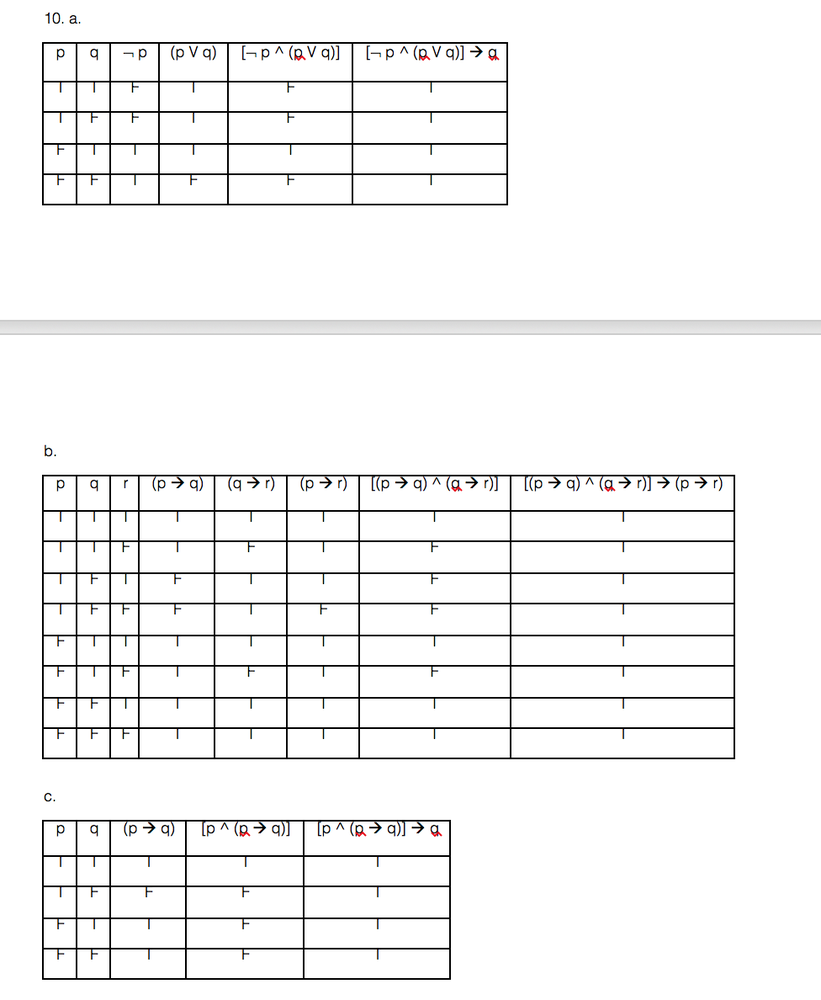
Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P

Artificial Intelligence Ppt Download

1 2 Propositional Equivalences 图文 百度文库
2

Produccion Final Logica Matematica Docsity

Chapter 1

Discrete Math Logic Proofs Conjecture 推測 By Danny Medium
2
2

Vin The Inverse Of The Proposition P Q Risa Pvq B P Q
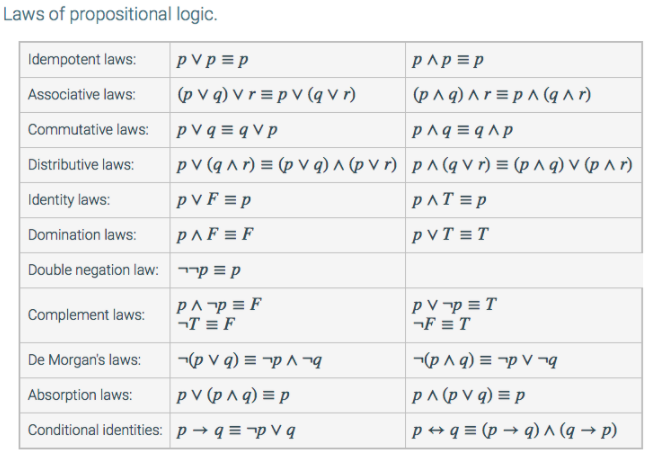
Solved Laws Of Propositional Logic Idempotent Laws P 3 P Chegg Com
4 4 Pts Construct A Truth Table For P V Q Could You Please Show Me How To Do This And Explain Your Steps I Am
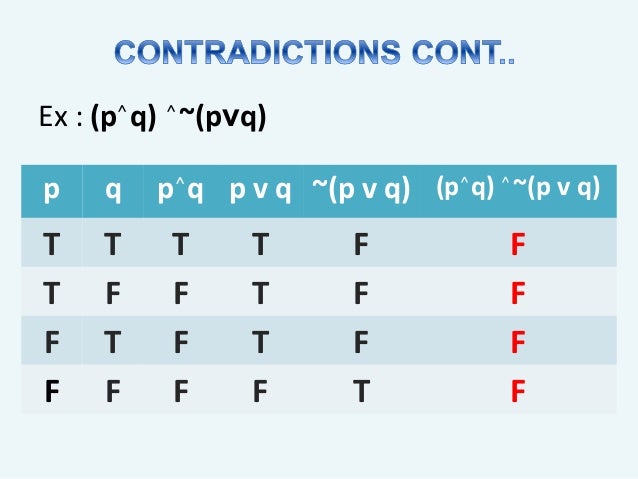
Logic Propositions
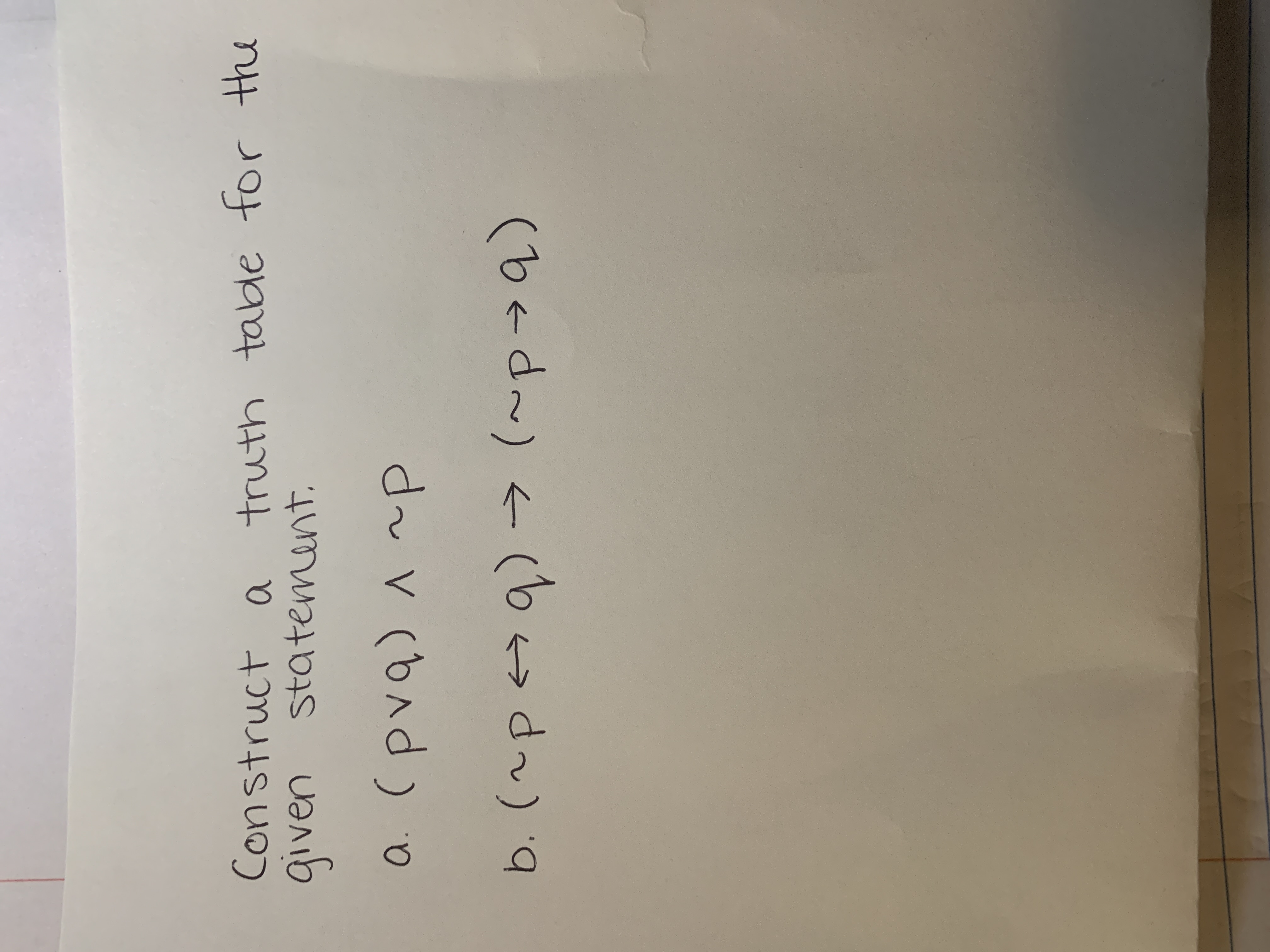
Jzcg44a877bjfm
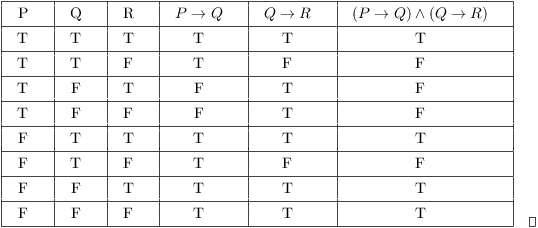
Truth Tables Tautologies And Logical Equivalences

Answered Fill In The Truth Table Q P Q Bartleby



